SOLVING SUDOKU
The One Rule:
- Fill in all blank cells making sure that each row, column and 3 by 3 box contains the numbers 1 to 9.
|
The Basics:
Firstly, it's impossible to get very far without carefully maintaining a list of 'possible values' or candidates for each blank cell. Doing this by hand is laborious and prone to error, and often detracts from the fun of solving these puzzles. Fortunately, programs like Simple Sudoku will do this for you, while leaving you with the fun of applying logic to solve each puzzle.
If you don't have a program to help - systematically analyse at each blank cell. Start with the assumption it can have any digit (or value) between 1 and 9, and then remove all values which have already been assigned to other cells in its respective row, column and 3x3 box. This leaves each blank cell with a list of candidates.
Repeat the following logical steps until the puzzle is solved. Only progress to more difficult steps when simpler steps neither reveal new values nor exclude candidates from blank cells.
|
Singles:
Any cells which have only one candidate can safely be assigned that value.
It is very important whenever a value is assigned to a cell, that this value is also excluded as a candidate from all other blank cells sharing the same row, column and box. (Programs like Simple Sudoku will do this laborious step automatically for you too.)
|  |
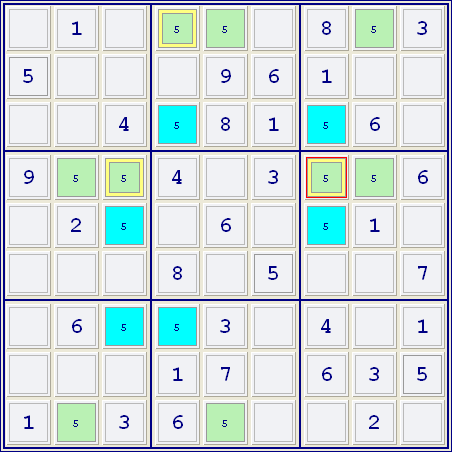
Hidden Singles:
Very frequently, there is only one candidate for a given row, column or box, but it is hidden among other candidates.
In the example on the right, the candidate 6 is only found in the middle right cell of the 3x3 box. Since every box must have a 6, this cell must be that 6.
|  |
Beyond the Basics:
While the two steps above are the only ones which will directly assign a cell value, they will only solve the simplest puzzles. That's fortunate, otherwise Sudoku wouldn't be as popular as it is today. The following steps (in increasing complexity) will reduce the number of candidates in blank cells so, sooner or later, a 'single' candidate or 'hidden single' candidate will appear.
Locked Candidates 1:
Sometimes a candidate within a box is restricted to one row or column. Since one of these cells must contain that specific candidate, the candidate can safely be excluded from the remaining cells in that row or column outside of the box.
In the example below, the right box only has candidate 2's in its bottom row. Since, one of those cells must be a 2, no cells in that row outside that box can be a 2. Therefore 2 can be excluded as a candidate from the highlighted cells.

|
Locked Candidates 2:
Sometimes a candidate within a row or column is restricted to one box. Since one of these cells must contain that specific candidate, the candidate can safely be excluded from the remaining cells in the box.
In the example on the right, the left column has candidate 9's only in the middle box. Therefore, since one of these cells must be a 9 (otherwise the column would be without a 9), 9's can safely be excluded from all cells in this middle box except those in the left column.
|
 |
Naked Pairs:
If two cells in a group contain an identical pair of candidates and only those two candidates, then no other cells in that group could be those values.
These 2 candidates can be excluded from other cells in the group.
In the example below, the candidates 6 & 8 in columns six and seven form a Naked Pair within the row. Therefore, since one of these cells must be the 6 and the other must be the 8, candidates 6 & 8 can be excluded from all other cells in the row (in this case just the highlighted cell).

|
Advanced Steps:
Naked Triples & Naked Quads:
The same principle that applies to Naked Pairs applies to Naked Triples & Naked Quads.
A Naked Triple occurs when three cells in a group contain no candidates other that the same three candidates. The cells which make up a Naked Triple don't have to contain every candidate of the triple. If these candidates are found in other cells in the group they can be excluded.
In the example on the right, a Naked Triple is formed by the top left, bottom left & bottom right cells of a box since they only contain the candidates 1, 4 & 6. Therefore the candidates 1 & 4 in the highlighted cells can be excluded safely.
|  |
A Naked Quad occurs when four cells in a group contain no candidates other that the same four candidates.
In the example on the right, the candidates 2, 5, 7 & 9 in the 3 left most cells and bottom middle cell of a box form a Naked Quad. Therefore candidates 5 & 7 that are in the highlighted cells can be excluded.
|  |
Hidden Pairs:
If two cells in a group contain a pair of candidates (hidden amongst other candidates) that are not found in any other cells in that group, then other candidates in those two cells can be excluded safely.
In the example on the right, the candidates 1 & 9 are only located in two highlighted cells of a box, and therefore form a 'hidden' pair. All candidates except 1 & 9 can safely be excluded from these two cells as one cell must be the 1 while the other must be the 9.
|  |
Hidden Triples:
If three candidates are restricted to three cells in a given group, then all other candidates in those three cells can be excluded.
In the example below, the candidates 3, 6 and 7 are found only in column four, six and seven. Therefore, all other candidates can be excluded from those three cells.
Hidden triples are generally extremely hard to spot but fortunately they're rarely required to solve a puzzle.

|
Hidden Quads:
If four candidates are restricted to four cells in a given group, then all other candidates in those four cells can be excluded.
Hidden Quads are very rare, which is fortunate since they're almost impossible to spot even when you know they're there.
Try and spot the Hidden Quad in the row below.
(Move your mouse over the image to reveal the answer).

|
For the Addict:
The following techniques are no more difficult than those above but requires observation as to how specific candidates relate to each other (in particular patterns) beyond any given row, column or box.
"X-Wing":
For every Sudoku, a value can exist only once in each row, column and box. If a value has only 2 possible locations in a given row (ie it has a candidate in only 2 cells in that row), then it must be assigned to one of these 2 cells. Given a particular puzzle that has two rows where a given candidate 'C' is restricted to exactly the same two columns (and no more than 2 columns), and since
1) candidate C must be assigned once in each of these two rows, and
2) no column can contain more than one of candidate C
then candidate C must be assigned exactly once in each of these two columns within these two rows. Therefore, it's not possible for any other cells in these two columns to contain candidate C. This same logic applies when a puzzle that has two columns where candidate C is restricted to exactly the same two rows.
This will be understood more easily by examining the example below. Filtering has been added so only candidate 6's are visible. (Cells which contain the filtered candidate are automatically highlighted pale green in Simple Sudoku unless subsequently recolored - which is the case for the blue cells this example).
The cells marked with a blue highlight form an "X-Wing" since rows one and nine both have only two cells with candidate 6's and these two cells share the same two columns. Therefore, other candidate 6's in columns six and nine (highlighted yellow) can safely be removed.
(Note: Candidate C must be assigned to either 1) the top-left and bottom-right corners, or 2) the bottom-left and top-right corners of the rectangular grid created by these two rows and columns. The pattern created by these crossed diagonals is the likely origin to this technique's name.)

|
"Swordfish":
The Swordfish pattern is a variation on the "X-Wing" pattern above.
Formal definition:
Given a particular puzzle that has three rows where a given candidate 'C' is restricted to the same three columns, and since
- candidate C must be assigned once in each of these three rows
- no column can contain more than one of candidate C
then candidate C must be assigned exactly once in each of these three columns within these three rows. Therefore, it's not possible for any other cells in these three columns to contain candidate C.
This same logic applies when a puzzle that has three columns where candidate C is restricted to exactly the same three rows.
In the example below, filtering has been added so only candidate 5's are visible.
Three rows (three, five & seven) have candidate 5 in no more than three cells (only two cells each in this example), and these cells all share the same three columns (three, four & seven). A "Swordfish" pattern is established. Other candidate 5's in these three columns (highlighted yellow) can be excluded safely.
Note: As shown in this example, there does not have to be exactly 3 cells in each row (or column), there may be less. However, there must not be more that three candidates in the pattern defining rows.
If you're particularly observant, you'll also spot the reciprocal Swordfish in the example above (which excludes the same candidates). Anyhow, it doesn't matter which Swordfish you spot first ...

Still confused? Click here for a bit more on Swordfish.
The X-Wing and Swordfish techniques can be further generalised to include rows containing candidates restricted to four cells in the same four columns (called a Jellyfish).
|
Solving with Colors:
Of interest are individual candidates which are in only two cells in a given group (a row, column or box). Those two cells have a 'conjugate' relationship where one must be the value (true) while the other must not (false). Because we don't yet know which is which, a recognised strategy is to visualise this relationship using two colors (and I've arbitrarily chosen blue and green for the following examples). Typically there are a number of 'conjugate pairs' present at any given time. Sometimes these conjugate pairs link with other conjugate pairs forming a chain of alternate true/false cell states, and these chains may expose candidates which can be excluded safely.
Whenever two cells in a conjugate chain have the same color and also share the same group, that color must be the 'false' color since each group can only have one of any value.
In the following example, filtering has been added so only candidate 9's are visible. (Cells which contain the filtered candidate are automatically highlighted pale green in Simple Sudoku unless subsequently recolored - which is the case for all but one cell in this example). It is easy to see that there are a number of conjugate relationships allowing alternate coloring in a chain. Starting with the cell R2C2, which I've arbitrarily colored green, it has 2 conjugates - cells R6C2 (since there are only 2 candidate 9's in Column 2) and cell R2C3 (since there are only 2 candidate 9's in row 2) which I've colored blue. Both these 2 blue cells (R6C2 & R2C3) have other conjugate cells which I've colored green. Repeating this technique around the grid we soon discover that there are blue cells sharing the same group. Since any group can only have one of a given value, the blue cells must represent the false values so all bright green cells can safely be assigned the value 9.

Also, whenever a candidate outside the chain relates by column, row or box to two alternately colored cells in a conjugate chain, that 'non-chain' candidate can be excluded.
This is best understood by looking at the example below. Filtering has been applied so only candidate 5's are visible. The cells labeled A & B form a conjugate pair as they are the only candidate 5's in column eight. Cells labelled B & C also form a conjugate pair as they are the only candidate 5's in the bottom right box. Finally, cells C & D form a conjugate pair as they are the only candidate 5's in row eight. As these three conjugate pairs all link together by separate conjugate relationships, they form a chain and can be colored alternately as shown. The yellow highlighted cell remotely relates to linked conjugate pairs of alternate colors (cells A & D). Since one of the two colors (blue & green) represents the true value 5, this remote candidate can safely be excluded.

Solving with Multi-Colors:
There are 2 types of what I call multi-colors. When filtering on a specific candidate and finding to 2 seperate conjugate chains (labelled Blue,Green & Pink,Orange respectively) ...
Type 1: If 'Blue' shares a group with 'Pink' and 'Orange' then 'Blue' must be the false candidate since either 'Pink' or 'Orange' must be true.
Example of Type 1:

Filtering on 7s and given that Blue & Bright Green are conjugate cells as are the Pink and Orange cells - then since either Pink or Orange must be 'true', then the Blue cells must be the 'false' cells since they share a group with both Pink and Orange. Candidate 7 can be excluded from all Blue cells.
Type 2: If 'Blue' shares a group with 'Orange' then any cell with the given candidate and sharing a group with both 'Green' and 'Pink' can have that candidate excluded. Reason: Since 'Blue' and 'Orange' can't both be true, then either one or both of 'Green' and 'Pink' must be true. Therefore any cell sharing a group with both 'Green' and 'Pink' can safely have that candidate excluded.
Example of Type 2:

Filtering on 4s and given that Blue & Bright Green are conjugate cells as are the Pink and Orange cells - then the Orange and Blue cells can't both be 'true' cells as they share a group. Therefore one or both of the Pink and Bright Green cells must be 'true' and, consequently, any cells which share a group with both Pink and Bright Green cells (ie r7c9) can have candidate 4 removed from that cell.
XY-Wing:
Not to be confused with X-Wing (see above).
Formal definition:
Given 3 cells where -
- all cells have exactly 2 candidates
- they share the same 3 candidates in the form - xy, yz, xz
- one cell (the Y 'stem' with canidates xy) shares a group with the other 2 cells (Y 'branches' with candidates xz & yz)
then any other cell which shares a group with both 'branch' cells can have excluded the 'z' candidate that is common to these 'branch' cells.
Note: If all 3 cells in a xy-wing pattern shared the same group, then they would be called a 'naked triple'.
Example:

R7C5 (A) is the 'stem' cell, and R1C5 (B) & R8C6 (C) are the 'branch' cells with candidate '5' common to both branches. Therefore, any cells which share a group with both these branches can safely have candidate 5 excluded (ie cells R1C6 & R9C5 as illustrated).
Finally, there are still other documented solving techniques (eg "Forcing Chains") which are beyond the scope of this webpage. There are some puzzles which can't be solved using simple logic and the only way to solve them is by resorting to trial-and-error. There are also some puzzles which have multiple solutions and are generally considered invalid or broken.
|
|
|