 Home
Home

 Home Home
|
Overview | 
|
By using an integer type for polygon coordinates, the Clipper Library has been able to avoid problems of numerical robustness that can cause havoc with geometric computations. Problems associated with integer rounding and their possible solutions are discussed below.
 It's important to stress at the outset that rounding causes vertices to move fractions of a unit away from their 'true' positions. Nevertheless, the resulting imprecision can be very effectively managed by appropriate scaling.
It's important to stress at the outset that rounding causes vertices to move fractions of a unit away from their 'true' positions. Nevertheless, the resulting imprecision can be very effectively managed by appropriate scaling.
The Clipper Library supports scaling to very high degrees of precision by accepting integer coordinate values in the range ±0x3FFFFFFFFFFFFFFF (± 4.6e+18).
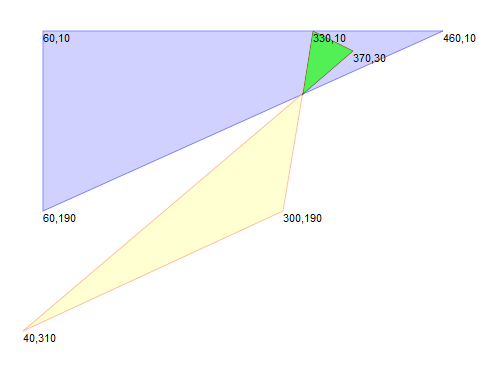
Another complication of using a discrete numbers (as opposed to real numbers) is that very occasionally tiny self-intersection artefacts arise. In the unscaled image on the left (where one unit equals one pixel), the area of intersection of two polygons has been highlighted in bright green.
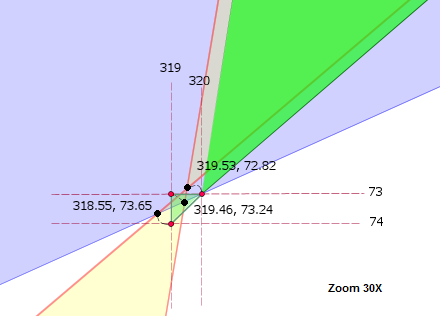
A 30X 'close up' of the lower points of intersection of these same two polygons shows the presence of a tiny self-intersecting artefact. The three 'black dots' highlight the actual points of intersection (with their fractional coordinates displayed). The 'red dots' show where these points of intersection are located once rounding is applied. With a little care you can see that rounding reverses the orientation of these vertices and causes a tiny self-intersecting artefact.
Although these tiny self-intersections are uncommon, if it's deemed necessary, they are best removed with CleanPolygons. (Setting Clipper's StrictlySimple property to true would also address this self-intersection but the tiny (sub-unit) polygon 'artefact' with incorrect orientation would still appear in the solution.)
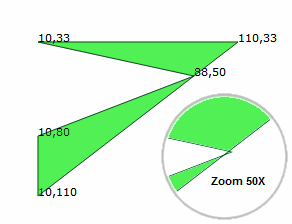
In this final example, the single polygon on the left also has a tiny self-intersection. However, the clipping algorithm sees this vertex (88,50) as simply 'touching' rather than intersecting the right edge of the polygon (though only by a fraction of a unit). Since this intersection won't normally be detected, the clipping solution (eg following a union operation) will still contain this tiny self-intersection. Setting Clipper's StrictlySimple property to true avoids this uncommon problem.
Clipper.StrictlySimple, CleanPolygons
Copyright ©2010-2022 Angus Johnson - Clipper2 6.4.2 - Help file built on 31-August-2022